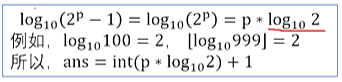刷题心得
floor函数
向下取整函数,返回值是double
还有一个就是 log 函数,这个是以 e 为底
洛谷1045
形如 $2^{P}-1$ 的素数称为麦森数,这时 $P$ 一定也是个素数。但反过来不一定,即如果 $P$ 是个素数,$2^{P}-1$ 不一定也是素数。到 1998 年底,人们已找到了 37 个麦森数。最大的一个是 $P=3021377$,它有 909526 位。麦森数有许多重要应用,它与完全数密切相关。
任务:输入 $P(1000<P<3100000)$,计算 $2^{P}-1$ 的位数和最后 $500$ 位数字(用十进制高精度数表示)
输入格式
文件中只包含一个整数 $P(1000<P<3100000)$
输出格式
第一行:十进制高精度数 $2^{P}-1$ 的位数。
第 $2\sim 11$ 行:十进制高精度数 $2^{P}-1$ 的最后 $500$ 位数字。(每行输出 $50$ 位,共输出 $10$ 行,不足 $500$ 位时高位补 $0$)
不必验证 $2^{P}-1$ 与 $P$ 是否为素数。
样例 #1
样例输入 #1
样例输出 #1
1
2
3
4
5
6
7
8
9
10
11
| 386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087
|
如何去分析呢,感觉太难了,不知道怎么处理
如何处理位数问题,就是取log以后向下取整加一就行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| #define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
const int N = 500;
typedef vector<int> vi;
vi a(N), res(N);
int ans = 0;
int p;
vi mul(vi& a, vi& b) {
vi t(N *2);
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
t[i + j] += a[i] * b[j];
t[i + j + 1] += t[i + j] / 10;
t[i + j] %= 10;
}
}
return t;
}
void quickpow(int p) {
res[0] = 1, a[0] = 2;
while (p)
{
if (p & 1) res = mul(res, a);
a = mul(a, a);
p >>= 1;
}
res[0]--;
}
int main() {
cin >> p;
quickpow(p);
ans = floor(p * log10(2)) +1;
cout << ans << endl;
for (int i = 499; i >=0; i--) {
if ((i + 1) % 50 == 0 && i!=499) cout << endl;
cout << res[i];
}
}
|
学习一下优先队列
默认是大根堆

1
2
3
4
5
| 有三个参数
第一个是类型
priority_queue<int,vector<int>,less<int> >
第二个是存储方式,第三个是规则,默认是大顶堆
改成小顶堆 great
|
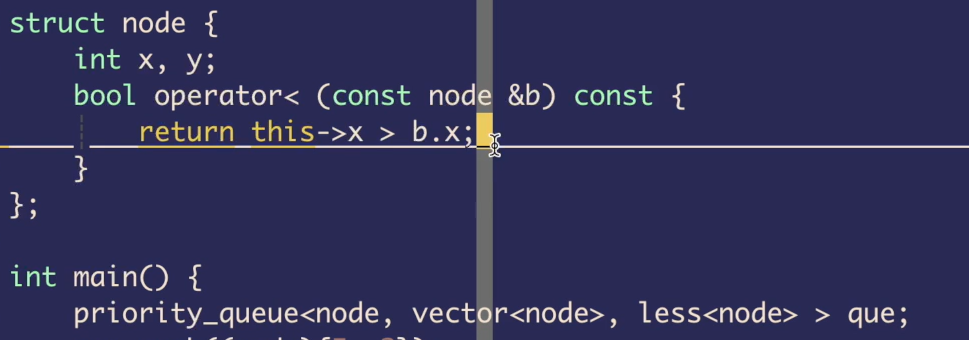
也可以用great,重载>
leecode 滑动窗口
这个题目可以用优先队列来实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
priority_queue<pair<int, int>> q;
for (int i = 0; i < k; i++) {
q.emplace(nums[i], i);
}
vector<int> ans={ q.top().first };
for (int i = k; i < n; i++) {
while (q.top().second <= i - k)
{
q.pop();
}
ans.push_back(q.top().first);
}return ans;
}
};
|
但是实际上还可以进一步优化,那些不能成为可能答案的点我们就没必要继续存储
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
deque<int> q;
for (int i = 0; i < k; ++i) {
while (!q.empty() && nums[i] >= nums[q.back()]) {
q.pop_back();
}
q.push_back(i);
}
vector<int> ans = {nums[q.front()]};
for (int i = k; i < n; ++i) {
while (!q.empty() && nums[i] >= nums[q.back()]) {
q.pop_back();
}
q.push_back(i);
if (q.front() <= i - k) {
q.pop_front();
}
ans.push_back(nums[q.front()]);
}
return ans;
}
};
|
蓝桥3522

这题需要用到欧拉函数,一个数 n ,其中小于等于 n 所包含的互质的数有 n (1-1/$p_1$) (1- $p_2$) … (1- $p_n$)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
#include <bits/stdc++.h>
using namespace std;
const int mod=998244353;
typedef unsigned long long ull;
ull quick_power(ull base,ull power,ull mod)
{
ull res=1;
while(power)
{
if(power&1)res=res*base%mod;
base=base*base%mod;
power=power>>1;
}
return res%mod;
}
ull Euler(ull n)
{
ull phi=n;
for(int i=2;i*i<=n;i++)
{
if(n%i)continue;
while(n%i==0)
{
n=n/i;
}
phi=phi/i*(i-1);
}
if(n>1)phi=phi/n*(n-1);
return phi;
}
int main()
{
ull a,b;
cin>>a>>b;
ull Euler_a=Euler(a);
ull ans=Euler_a*quick_power(a,b-1,mod)%mod;
cout<<ans<<endl;
return 0;
}
|
落谷 1462

所有类似于“求解所有的最大值中的最小值”的问题,都应该先想一想用二分答案的方法来写。
啊啊啊啊,不会写
洛谷 1419

我们要学会如何自己用一个数组去维护一个双端队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| #define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, s, t;
double p[N];
double pre[N];
int q[N];
bool check(double x) {
pre[0] = 0;
for (int i = 1; i <= n; i++) {
pre[i] = pre[i - 1] + p[i] - x;
}
int h = 0, tt = 1;
for (int i = s; i <= n; i++) {
while (h>=tt&&pre[q[h]]>pre[i-s])
{
--h;
}
q[++h] = i - s;
while (h>=tt&&i-q[tt]>t)
{
++tt;
}
if (h >= tt && pre[i] - pre[q[tt]] >= 0) return true;
}
return false;
}
double find()
{
double l = -10000, r = 1000 * n;
while (r-l>1e-5)
{
double mid = (l + r) / 2;
if (check(mid)) l = mid;
else r = mid;
}
return l;
}
int main() {
cin >> n >> s >> t;
for (int i = 1; i <= n; i++) {
cin >> p[i];
}
printf("%.3lf", find());
}
|
P1352 没有上司的舞会
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include<bits/stdc++.h>
using namespace std;
int n;
long long r[6005];
vector<long long> son[6005];
long long f[6005][2];
long long ans = 0;
int isf[6005];
void dfs(int u){
f[u][1] = r[u];
for(int i=0;i<son[u].size();i++){
int dd = son[u][i];
dfs(dd);
f[u][0] += max(f[dd][0],f[dd][1]);
f[u][1] += f[dd][0];
}
}
int main(){
cin >> n;
for(int i=1;i<=n;i++){
cin >> r[i];
}
int l,k;
for(int i=1;i<n;i++){
cin >> l >> k;
son[k].push_back(l);
isf[l] = 1;
}
int num = 1;
while(isf[num]) num++;
dfs(num);
cout << max(f[num][0],f[num][1]);
return 0;
}
|
树中的最大直径
树的直径一般用树形 DP 或两次 DFS 的方式求解,我这里使用的是两次 DFS。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| const int N = 10000 + 10;
int n, c, d[N];
vector<int> E[N];
void dfs(int u, int fa) {
for (int v : E[u]) {
if (v == fa) continue;
d[v] = d[u] + 1;
if (d[v] > d[c]) c = v;
dfs(v, u);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d %d", &u, &v);
E[u].push_back(v), E[v].push_back(u);
}
dfs(1, 0);
d[c] = 0, dfs(c, 0);
printf("%d\n", d[c]);
return 0;
}
|
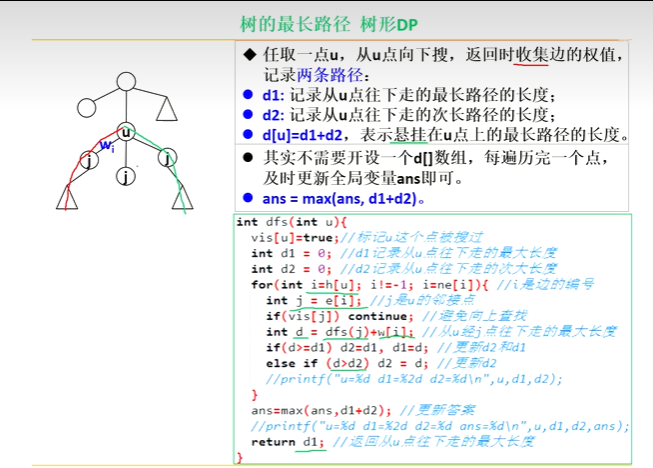
树形dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include<bits/stdc++.h>
using namespace std;
const int N = 10010,M = N*2;
int n,ans;
bool vis[N];
int head[N],edge[M],w[M],ne[M],idx;
void add(int a,int b,int c){
edge[++idx] = b;
w[idx] = c;
ne[idx] = head[a];
head[a] = idx;
}
int dfs(int u){
vis[u] = true;
int d1 = 0,d2 = 0;
for(int i=head[u];i!=-1;i = ne[i]){
int j = edge[i];
if(vis[j]) continue;
int d = dfs(j) + w[i];
if(d>=d1) d2 = d1,d1=d;
else if(d>d2) d2 = d;
}
ans = max(ans,d1+d2);
return d1;
}
int main(){
memset(head,-1,sizeof head);
cin >> n;
for(int i=1;i<n;i++){
int a,b,c;
cin >> a >> b >> c;
add(a,b,c);
add(b,a,c);
}
dfs(1);
cout << ans*10+ans*(ans+1)/2;
return 0;
}
|
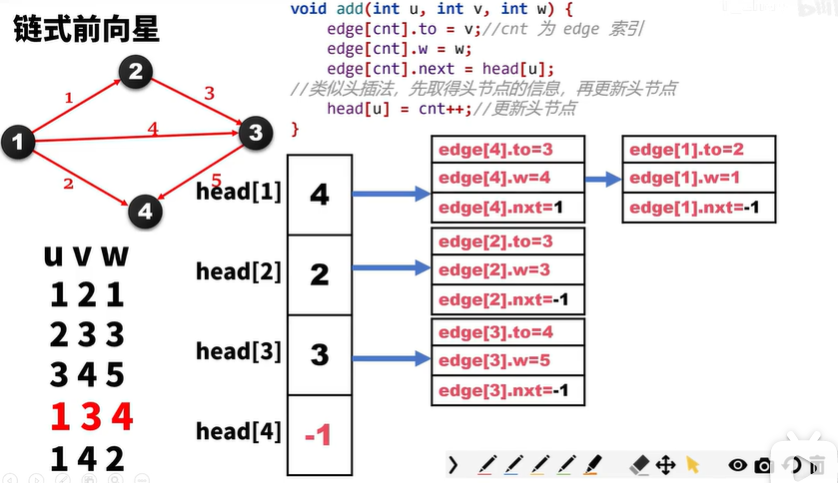
链式前向星
头插法,next可以理解为指针,如果指向-1,则后面没有数据
head[i]数组是以i为起点的第一条边的存储位置
edge是一个边集合